Question

Small pizzas at Ponnie's Pizza are cut into 6 pieces. The circumference of a small pizza is 12π inches. A large pizza is cut into 8 pieces. The diameter of a large pizza is 16 inches.

Joannie eats 2 slices of a small pizza. Mark eats 5 slices of a large pizza.

How many times greater are the square inches of pizza that Mark ate than the square inches of pizza that Joannie ate?

Enter your answer, rounded to the nearest tenth, in the box.

Answer 1

Mark ate 3.3 times the square inches of pizza than Joannie ate.

Explanation:

Small pizza

The formula for the circumference of a circle is C = 2πr (where r is the radius). If the circumference of a small pizza is 12π inches, then its radius is:

`\implies \sf Radius_(small\;pizza)=(circumference)/(2\pi)=(12\pi)/(2\pi)=6\;inches`

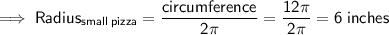
The formula for the area of a circle is A = πr² (where r is the radius).

Therefore, the area of a small pizza is:

`\implies \sf Area_(small\;pizza)=\pi \cdot 6^2=36\pi \; in^2`

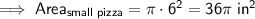
If the small pizzas are cut into 6 congruent pieces, the area of one slice of small pizza is:

`\begin{aligned}\implies \sf Area_(small\;slice)&=\sf (Area_(small\;pizza))/(6)\\\\&=(36 \pi)/(6)\\\\&=6 \pi \; \sf in^2\end{aligned}`

Therefore, the area of one slice of small pizza is 6π square inches.

`\hrulefill`

Large pizza

The diameter of a circle is twice its radius.

If the diameter of a large pizza is 16 inches then its radius is:

`\implies \sf Radius_(large\;pizza)=(diameter)/(2)=(16)/(2)=8\;inches`

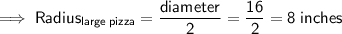
The formula for the area of a circle is A = πr² (where r is the radius).

Therefore, the area of a large pizza is:

`\implies \sf Area_(large\;pizza)=\pi \cdot 8^2=64 \pi \; in^2`

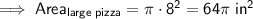
If the large pizzas are cut into 8 congruent pieces, the area of one slice of large pizza is:

`\begin{aligned}\implies \sf Area_(large\;slice)&=\sf (Area_(large\;pizza))/(8)\\\\&=(64 \pi)/(8)\\\\&=8 \pi \; \sf in^2\end{aligned}`

Therefore, the area of one slice of large pizza is 8π square inches.

`\hrulefill`

If Joannie eats 2 slices of small pizza, the square inches of pizza she ate is:

`\implies \sf Joannie=2 * 6 \pi = 12 \pi\;in^2`

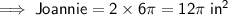
If Mark eats 5 slices of large pizza, the square inches of pizza he ate is:

`\implies \sf Mark =5 * 8 \pi = 40\pi\;in^2`

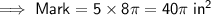
To calculate how many times greater are the square inches of pizza that Mark ate than the square inches of pizza that Joannie ate, divide the area Mark ate by the area Joannie ate:

`\implies \sf (40 \pi)/(12 \pi) = (10)/(3)=3.3\;(nearest\;tenth)`

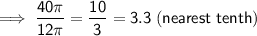
Therefore, Mark ate 3.3 times the square inches of pizza than Joannie ate.