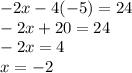Question

3 Use the system of equations shown.

-2x - 4y= 24
6x-8y=28
a. How could you change one of the equations so that you could add it to the
other equation and eliminate the x terms?
b. How could you change one of the equations so that you could add it to the
other equation and eliminate the y terms?
c. What is the solution of the system? Show your work.

Answer 1

a. Multiply the entire first equation by 3 so that the xs will be eliminated when the two equations are added.

b. Multiply the entire first equation by -2 so that the ys will be eliminated when the two equations are added.

c. y = -5; x = -2

Explanation:

a. We're able to cancel a variable when the two variables are the same number with opposite signs (e.g., -3 + 3 = 0, -80 + 80 = 0)

If we multiply the entire first equation by 3, we get

`3(-2x-4y=24)\\-6x-12y=72`

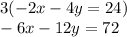
-6x + 6x = 0

b. We can again use the first equation and multiply it by -2 to cancel out the ys:

`-2(-2x-4y=24)\\4x+8y=-48`

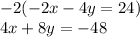
8y - 8y = 0

c. We can first solve for y by first canceling the xs using the process in part a.

`3(-2x-4y=24)\\\\\\-6x-12y=72\\6x-8y=28\\\\-20y=100\\y=-5`

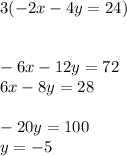
We can now plug in -5 for y into the first equation to find x:

`-2x-4(-5)=24\\-2x+20=24\\-2x=4\\x=-2`