Question

Help with this problem guys
no trolling please i really need it

Answer 1

`\textsf{1.}\quad \sf \overline{AZ} = 28 \; meters`

`\textsf{2.}\quad \sf \overline{AM} = 28 \; meters`

`\textsf{3.}\quad b = \sf 4`

`\textsf{4.}\quad \sf Perimeter = 112\; meters`

`\textsf{5.}\quad \sf \overline{MX} = 22\; meters`

`\textsf{6.}\quad \sf \overline{AX} = 10√(3)\; meters`

`\textsf{7.}\quad \sf \overline{EX} = 10√(3)\; meters`

`\textsf{8.}\quad \sf \overline{AE} = 20√(3)\; meters`

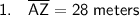
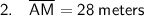
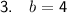
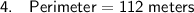
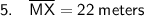
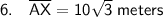
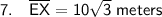
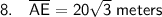
Explanation:

Side lengths and value of b

All sides of a rhombus are the same length. Therefore, for rhombus MAZE:

`\sf \overline{AZ} = \overline{AM} = \overline{ZE} = \overline{EM}`

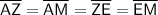
Given:

• 
  `\overline{\sf AZ} =8b-4`

• 
  `\overline{\sf AM} =5b+8`

As the sides of a rhombus are the same length, we can equate the expressions for sides AZ and AM, and solve for b:

`\begin{aligned}\overline{\sf AZ}&=\overline{\sf AM}\\8b-4&=5b+8\\8b-4-5b&=5b+8-5b\\3b-4&=8\\3b-4+4&=8+4\\3b&=12\\3b / 3&=12 / 3\\b&=4\end{aligned}`

Therefore, the value of b is 4.

To find the length of AZ and AM, substitute the found value of b into one of the expressions:

`\begin{aligned}\overline{\sf AZ}&=8b-4\\&=8(4)-4\\&=32-4\\&=28\end{aligned}`

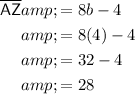
Therefore, as AZ = AM, then AZ = 28 and AM = 28.

`\hrulefill`

Perimeter

As the sides of a rhombus are equal in length, each side length is 28 meters (as found previously).

The perimeter of rhombus MAZE is the sum of its side lengths. Therefore:

`\begin{aligned}\sf Perimeter\;MAZE&=\sf \overline{AZ} +\overline{AM} +\overline{ZE}+ \overline{EM}\\&=28+28+28+28\\&=112\; \sf meters\end{aligned}`

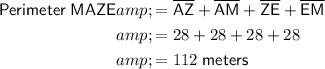
Therefore, the perimeter of rhombus MAZE is 112 meters.

`\hrulefill`

Diagonals

The point of intersection of the diagonals of rhombus MAZE is point X.

As the diagonals of a rhombus are perpendicular bisectors of each other, then:

`\sf \overline{AX}=\overline{EX}\quad and \quad \overline{AX}+\overline{EX}=\overline{AE}`

`\sf\overline{MX}=\overline{ZX}\quad and \quad\overline{MX}+\overline{ZX}=\overline{MZ}`

Given MZ = 44 meters, and MX is half of MZ, then:

`\sf \overline{MX}=\overline{ZX}=22\;meters`

As the diagonals bisect each other at 90°, m∠MXA= 90°. Therefore, ΔMXA is a right triangle with hypotenuse AM = 28 and leg MX = 22.

As we know the lengths hypotenuse AM and leg MX, we can use Pythagoras Theorem to calculate the length of the other leg, AX:

`\begin{aligned}\sf \overline{AX}^2+\overline{MX}^2&=\sf \overline{AM}^2\\\sf \overline{AX}^2+22^2&=\sf 28^2\\\sf \overline{AX}^2&=\sf 28^2-22^2\\\sf \overline{AX}&=√(\sf 28^2-22^2)\\\sf \overline{AX}&=\sf 10√(3)\; meters\end{aligned}`

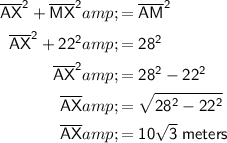
As the diagonals bisect each other, AX = EX. Therefore:

`\sf \overline{EX}=\sf 10√(3)\; meters`

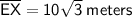
The length of diagonal AE is the sum of segments AX and EX. Therefore:

`\begin{aligned}\sf \overline{AE}&=\sf \overline{AX}+\overline{EX}\\&=\sf 10√(3)+10√(3)\\&=\sf 20√(3)\; meters\end{aligned}`

`\hrulefill`

Note: The attached diagram is drawn to scale.