Question

(2,90) and (4,810) as an exponential function

Answer 1

y = 10(3)^x

Explanation:

The general form of an exponential function is

`y=ab^x`, where x and y are any coordinate in the exponential function, a is the initial value, and b is the base.

Currently, we only have xs and ys, which forces us to find a and b:

`90=ab^2\\810=ab^4`

We can find b first by dividing the larger x and y (4, 810) by the smaller x and y (2, 90). Thus, we must plug the xs and ys in and create a fraction:

`(810)/(90)=(ab^4)/(ab^2)`

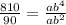
We know that a represents a value a number divided by itself is 1 and that 810/90 = 9 so we now have:

`9=(b^4)/(b^2)`

According to quotient rule of exponents, when you divide bases with exponents, you subtract the exponent on the numerator from the base on the denominator:

`9=b^4^-^2\\9=b^2\\3=b`

Now we can simply plug in our first coordinate and 3 for b to find a:

`90=a(3)^2\\90=9a\\10=a`

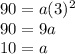
Thus, the equation of the exponential function which contains the points (2,90) and (4,810) is

y = 10(3)^x