Question

Describe the transformation of the graph of the parent quadratic function then identify the vertex

Answer 1

The vertex of a quadratic function can be found by the following expression:

`x=(-b)/(2a)`

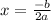
When we add a number to the argument of the function, "x", we shift the function left or right. If the number is positive the shift happens to the left, if is negative the shift happens to the right.

When we add a number to the whole function we shift the function up or down. If the number is positive the shift is on the upwards direction and if it is negative the shift is on the downwards direction.

When we multiply a function we are stretching or compressing it. If the number is greater than 1, we are compressing the function and if its smaller than 1 we are stretching i.

With this in mind we can find which transformations happened in each option. The original function is:

`f(x)=x^2`

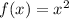
27.

`f(x)=3(x+2)^2+1`

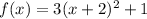
There is a number 3 multiplying the function, so it got compressed by a factor of three. There is a number 2 adding to the variable, so it got shifted left by 2. There is a number 1 adding the whole function, so it got moved upwards by 1.

The vertex of the original function is at (0,0). The function moved upwards by 1 this happens on the y-axis and left by 2 this happens on the x-axis, so the new vertex is (-2,1).

28.

`f(x)=-4(x+1)^2-5`

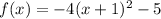
There is a negaive number, "-4", multiplying the function, so it got compressed by a factor of four and it also got inverted, because the number is negative. There is a number "1" adding the variable, so it got moved one unit to the left. There is a number "-5" adding the whole function, so it got moved five units down.

Since the function moved one unit to the left, changing the x-coordinate for the vertex by "-1" and it also moved five units down, changing the y-coordinate for the vertex by "-5", the new vertex is (-1, -5).

29.

`f(x)=-2x^2+5`

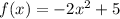
There is a negative number multiplying the function, so it got compressed by a factor of 2 and inverted. There is also a constant adding to the function, so it got moved up by 5 units.

Since the function didn't moved in the x-axis, but got up 5 units on the y-axis the new vertex is (0,5).

30.

`f(x)=(1)/(2)(x-1)^2`

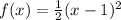
There is a number "1/2" multiplying the function, since it is lower than 1, the function got stretched by a factor of 2. There is a constant adding "-1" to the variable, therefore the function got moved to the right by one unit.

Since the function moved 1 unit to the right the new vertex is (1,0).