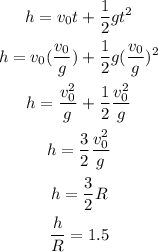Question

Consider an airless, non-rotating planet of mass M and radius R. and electromagnetic launcher standing on the surface of this planet shoots a projectile with initial velocity v0 directed straight up. Unfortunately, due to some error, v0 is less than the planet's escape velocity ve; specifically, v0 = 0.762ve. Unable to escape the planet's gravitational pull, the projectile rises to a maximal height h above the ground, then falls back to the ground. Calculate the ratio h/R of the projectile's maximum height to the planet's radius.

Answer 1

1.39

Step-by-step explanation:

(1/2)mVe^2=(mMG)/R
Ve^2=2MG/R

(1/2)mVo^2=mMG(1/R-1/(R+h))=mMG(h/(R^2+Rh))

Vo^2=2MG(1/R)(h/(R+h))
Vo^2=Ve^2(h/(R+h))

Vo^2/Ve^2=h/(R+h)
Ve^2/Vo^2=(R+h)/h
1/.762^2=(R+h)/h

1.72h-h=R

.72h=R

h/R=h/.72h
h/R=1.39

Answer 2

Given data:

The mass of planet is M.

The radius of planet is R.

The initial velocity of projectile is v₀=0.762ve.

The amount of kinetic and potential energy should be equal according to conservation of energy,

`\begin{gathered} KE=PE \\ (1)/(2)mv^2_e=(GMm)/(R)^{}_{} \\ R=\frac{GM^{}_{}}{v^2_e} \end{gathered}`

The escape velocity is given by,

`v_e=\sqrt[]{(2GR)/(M)}`

Here, G is the universal gravitational acceleration.

The time taken to reach the maximum height will be,

`\begin{gathered} v_0=gt \\ t=(v_0)/(g) \end{gathered}`

The maximum height reached by the projectile is given by,

`\begin{gathered} h=v_0t+(1)/(2)gt^2 \\ h=v_0((v_0)/(g))+(1)/(2)g((v_0)/(g))^2 \\ h=(v^2_0)/(g)_{}+(1)/(2)(v^2_0)/(g)_{} \\ h=(3)/(2)(v^2_0)/(g)_{} \\ h=(3)/(2)R \\ (h)/(R)=1.5 \end{gathered}`