Question

A 5.0g bullet is fired straight up from the ground, The bullet leaves the ground with a speed of 85 m/s taking to the ground as the reference levelA) what is the gravitational P.E of the bulletB) what is the initial KE of the bulletC) what is the total initial ME of the bullet when the bullet is 12m high above the groundD) what is the gravitational PE of the bulletE) what should the ME be at this height F) how fast is the bullet moving at this height

Answer 1

Given information:

Mass of the bullet;

`\begin{gathered} m=5\text{ g} \\ =5*10^(-3)\text{ kg} \end{gathered}`

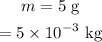
Initial velocity of the bullet;

`u=85\text{ m/s}`

Part (a),

Taking ground as the reference level. So, the initial height of the bullet is 0 m.

The gravitational potential energy is given as,

`U=\text{mgh}`

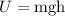
Here, g is the acceleration due to gravity.

Substituting all known values,

`\begin{gathered} U=(5*10^(-3)\text{ kg})*(9.8\text{ m/s}^2)*0 \\ =0\text{ J} \end{gathered}`

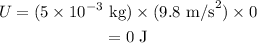
Therefore, the gravitational potential energy at the ground is 0 J.

Part (B)

The initial kinetic energy of the bullet is given as,

`K=(1)/(2)mu^2`

Substituting all known values,

`\begin{gathered} K=(1)/(2)*(5*10^(-3)\text{ kg})*(85\text{ m/s})^2 \\ =18.0625\text{ J} \end{gathered}`

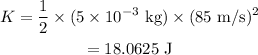
Therefore, the initial kinetic energy of the bullet is 18.0625 J.

Part (C).

According to the conservation of energy, the total mechanical energy (ME) of the bullet will remain conserved. Therefore, the total initial ME of the bullet when the bullet is 12 m high above the ground is 18.0625 J.

Part (D)

The gravitational potential energy when the bullet is 12 m high is,

`U_h=mgh`

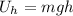
Substituting all known values,

`\begin{gathered} U_h=(5*10^(-3))*(9.8\text{ m/s}^2)*(12\text{ m}) \\ =0.588\text{ J} \end{gathered}`

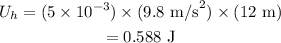
Therefore, the gravitational potential energy when the bullet is 12 m high is 0.588 J.

Part (E).

The velocity of the bullet when it reaches the height of 12 m is given as,

`v^2=u^2-2gh`

Here, v is the velocity when the bullet is 12 m high.

Substituting all known values,

`\begin{gathered} v^2=(85\text{ m/s})^2-2*(9.8\text{ m/s})*(12\text{ m}) \\ =6989.8\text{ m}^2\text{ /s}^2 \end{gathered}`

The total mechanical energy when the bullet is 12 m high is,

`ME=U_h+(1)/(2)mv^2`

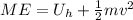
Substituting all known values,

`\begin{gathered} ME=(0.588\text{ J})+(1)/(2)*(5*10^(-3)\text{ kg})*(6989.8\text{ m}^2\text{ /s}^2) \\ =18.0625\text{ J} \end{gathered}`

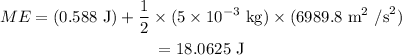
Therefore, the total mechanical energy ME when the bullet is 12 m high is 18.0625 J.

Part (F),

The velocity when the bullet is 12 m high is given as,

`v=\sqrt[]{u^2-2gh}`

Substituting all known values,

`\begin{gathered} v=\sqrt[]{(85\text{ m/s})^2-2*(9.8\text{ m/s}^2)*(12\text{ m})} \\ \approx83.605\text{ m/s} \end{gathered}`

Therefore, the velocity when the bullet is 12 m high is 83.605 m/s.