Question

Two machines worked on a car. The first mechanic worked for 20 hours, and the second mechanic worked for 15 hours. Together they charge a total of $2250. What was the rate charged per hour by each mechanic if the sum of the two rates was $125 per hour?

Answer 1

Let's make,

mechanic #1's rate = x

mechanic #2's rate = y

Note that their rate is dollars per hour.

Now, mechanic #1 worked for 20 hours. Then, we get the following equation:

20x = money earned by mechanic #1

On the other hand, mechanic #2 worked for 15 hours. Then, we get the following equation:

15y = money earned by mechanic #2

together they charged a total of $2250. So the amount of money earned by both mechanics is:

20x + 15y = 2250 EQUATION 1

On the other hand, the sum of the two rates was:

x + y = 125 EQUATION 2

From the equation, if we solve for x, we get:

x = 125-y EQUATION 3

plug (125-y) in for "x" in equation 1 to get everything in terms of one variable:

20(125-y)+15y = 2250

this is equivalent to

2500-20y +15y = 2250

this is equivalent to

2500 -5y = 2250

this is equivalent to

-5y = 2250 -2500

this is equivalent to:

-5y = -250

or

5y = 250

solving for y, we get:

`y\text{ =}(250)/(5)=50`

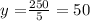
now, replacing this into equation 3, we get:

x = 125-y = 125 - (50) = 75

so that, we can conclude that the correct answer is:

mechanic #1 charged 75 $/hr

mechanic #2 charged 50 $/hr