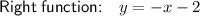Question

asked May 25, 2024 150k views

2 Answers

Marthe · Answer 1 · 2024-05-27T11:09:48+0000

Answer:

D

Explanation:

the slope of the function on the left is
(1)/(2) . so, if the slope multiplied by -2 we got -1.

y-intercept is at 1. if 1 plus -3 we got -2

Deanmcpherson · Answer 2 · 2024-05-30T20:59:34+0000

Answer:

$\textsf{D.\quad$p=-2$\;\;and\;\;$q=-3$}$

Explanation:

The slope of a line shows the direction and steepness of the line.

The slope of a line can by calculated by using slope formula:

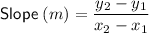
$\textsf{Slope\;$(m)=(y_2-y_1)/(x_2-x_1)$}$

where (x₁, y₁) and (x₂, y₂) are two points on the line.

Given the left function passes through the points (4, 3) and (0, 1), substitute these into the slope formula to find the slope of the line:

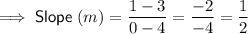
$\implies \textsf{Slope}\;(m)=(1-3)/(0-4)=(-2)/(-4)=(1)/(2)$

Given the righ-5 function passes through the points (-5, 3) and (-2, 0), substitute these into the slope formula to find the slope of the line:

$\implies \textsf{Slope}\;(m)=(0-3)/(-2-(-5))=(-3)/(3)=-1$

Given the slope of the function on the left is multiplied by p to arrive at the slope of the function on the right:

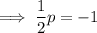
$\implies (1)/(2)p=-1$

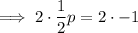
$\implies 2 \cdot (1)/(2)p=2 \cdot -1$

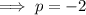
$\implies p=-2$

The y-intercept is the point at which the line crosses the y-axis.

The left function crosses the y-axis at (0, 1), so its y-intercept is y = 1.

The right function crosses the y-axis at (0, -2), so its y-intercept is y = -2.

Given q is added to the y-intercept of the function on the left to arrive at the y-intercept of the function on the right:

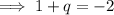
$\implies 1+q=-2$

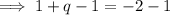
$\implies 1+q-1=-2-1$

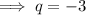
$\implies q=-3$

$\textsf{$p=-2$\;\;and\;\;$q=-3$}$

The equations of the functions are:

$\textsf{Left\;function:\quad $y=(1)/(2)x+1$}$

$\textsf{Right\;function:\quad $y=-x-2$}$

Please log in or register to add a comment.