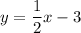Question

Write an equation in slope-intercept form of the line that passes through the given point and parallel to the given line. (-4,-5); y=1/2x-6 ASAP PLS

Answer 1

`y=(1)/(2)x-3`

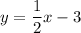
Explanation:

The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.

Given line:

`y=(1)/(2)x-6`

The given line is in slope-intercept form. Therefore:

• slope = ¹/₂
• y-intercept = -6

The slopes of parallel lines are the same.

Therefore, the slope of a line parallel to the given line is also ¹/₂.

Given the parallel line passes through the point (-4, -5), substitute this and the found slope into the slope-intercept formula and solve for b:

`\implies y=mx+b`

`\implies -5=(1)/(2)(-4)+b`

`\implies -5=-2+b`

`\implies b=-3`

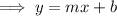
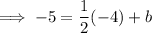
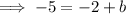
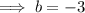
Therefore, the equation of the line that passes through the given point and is parallel to the given line in slope-intercept form is:

`y=(1)/(2)x-3`