Answer:
16 x = 2
17.
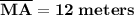
18.

19.
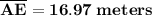
20. Perimeter = 48 meters
*** Please look at my comment on question 20 at the very bottom of the explanation
Explanation:
Since the given figure is a square, all four sides must be equal
Therefore
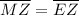
Plugging in given expressions for
 we get:
we get:
5x + 2 = 9x -6
Subtract 5x from both sides:
5x - 5x + 2 = 9x - 5x -6
2 = 4x - 6
Add 6 both sides:
2 + 6 = 4x - 6 + 6
8 = 4x
Switch sides:
4x = 8
Divide both sides by 4:
4x/4 = 8/4
x = 2 (Answer #16)
Therefore
Keeping in mind that all four sides are equal,
 (Answer # 17)
(Answer # 17)
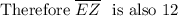
(Can verify this with plugging in x =2 into 9x - 6 giving
9(2) - 6 = 18 - 6 =12
and also ME =12)
To find
 since MZ is the diagonal and the angles of a square are all 90°,
since MZ is the diagonal and the angles of a square are all 90°,
in ΔMZE, MZ is the hypotenuse of a right triangle with legs ME and EZ
Therefore
MZ² = ME² + EZ²
= 12² + 12²
= 2 (12²)
Therefore
 since √a² = a
since √a² = a
 (Answer #18)
(Answer #18)
In a square the diagonals are equal so
 (Answer #19)
(Answer #19)
Perimeter of the square = 4 x length of each side
= 4 x 12
= 48 meters (Answer #20)
*** In question 20 which is rather confusing, I have taken only the outer edges of the square
If they mean the length of all lines including the diagonals which make up the maze, you will have to add the two diagonals which means 48 + 16.97 + 16.97 = 81.94 meters
Perimeter refers to the outer edges so I believe the answer of 48 is correct. Just not 100% sure on this. Sorry