Answer:
A) The solid resulting from rotating the right triangle around the x-axis is a cone. The height of the cone is equal to the horizontal distance between vertex K and vertex L, which is 9 units. The radius of the circular base of the cone is equal to the vertical distance between vertex K and vertex J, which is 2 units.
B) The volume of the resulting solid is 37.7 cubic units (to the nearest tenth).
Explanation:
Given a right triangle with vertices J (0, 2), K (0, 0), and L (9, 0) is rotated around the x-axis.
Part A
The solid resulting from rotating the right triangle around the x-axis is a cone.
The height of the cone is equal to the horizontal distance between vertex K and vertex L, which is 9 units.
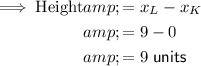
The radius of the circular base of the cone is equal to the vertical distance between vertex K and vertex J, which is 2 units.
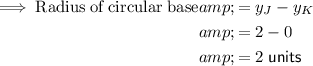
Part B
To calculate the volume of the cone, we can use the formula:

where r is the radius of the circular base and h is the height of the cone.
From part A, the values are:
Substitute the values into the formula and solve for V:
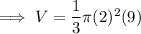
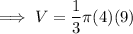
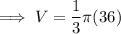
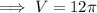
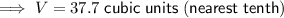
Therefore, the volume of the resulting solid is 37.7 cubic units (to the nearest tenth).