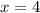Question

Solve for x.
2log₂x = 3 + log₂(x-2)

Answer 1

x = 4

Explanation:

1) Use Power Rule:
`\text{log}_bx^c=c\text{log}_bx`.

`\text{log}_2x^2=3+\text{log}_2(x-2)`

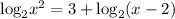
2) Move all terms to one side.

`\text{log}_2x^2-3-\text{log}_2(x-2)=0`

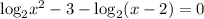
3) Use Quotient Rule:
`\text{log}_b(x)/(y) =\text{log}_bx-log_by`.

`\text{log}_2((x^2)/(x-2) )-3=0`

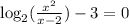
4) Add 3 to both sides.

`\text{log}_2((x^2)/(x-2))=3`

5) Use Definition of Common Logarithm:
`b^a=x` if and only
`\text{log}_b(x)=a`.

`(x^2)/(x-2) =2^3`

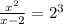
6) Simplify
`2^3` tom 8.

`(x^2)/(x-2) =8`

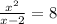
7) Multiply both sides by x - 2.

`x^2=8(x-2)`

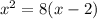
8) Expand.

`x^2=8x-16`

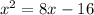
9) Move all terms to one side.

`x^2-8x+16=0`

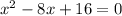
10) Rewrite
`x^2-8x+16` in the form
`a^2-2ab+b^2`, where
`a=x` and
`b=4.`

`x^2-2(x)(4)+4^2=0`

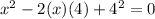
11) Use Square of Difference:
`(a-b)^2=a^2-2ab+b^2`.

`(x-4)^2=0`

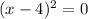
12) Take the square root of both sides.

`x-4=0`

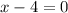
13) Add 4 to both sides.

`x=4`