We are given the following expression:
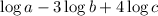
we are asked to simplify this expression. To do that we will first use the following property:
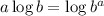
we will apply this to the second and third terms, like this:
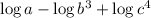
Now we will use the following property:
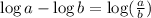
we will use this property for the first and second terms:
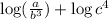
Now we will use the following property:
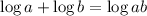
We will use the property in the last two terms, like this:
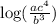
And thus, we have simplified the logarithmic expression into one single logarithm