Question

use the product, quotient, and power rules of logarithms to rewrite the equation as a single logarithm.

Answer 1

We are given the following expression:

`\log a-3\log b+4\log c`

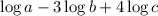
we are asked to simplify this expression. To do that we will first use the following property:

`a\log b=\log ^{}b^a`

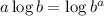
we will apply this to the second and third terms, like this:

`\log a-\log b^3+\log c^4`

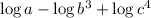
Now we will use the following property:

`\log a-\log b=\log ((a)/(b))`

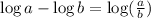
we will use this property for the first and second terms:

`\log ((a)/(b^3))+\log c^4`

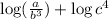
Now we will use the following property:

`\log a+\log b=\log ab`

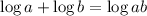
We will use the property in the last two terms, like this:

`\log ((ac^4)/(b^3))`

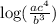
And thus, we have simplified the logarithmic expression into one single logarithm