Question

Find cos2θ if sinθ=5/13

Answer 1

Answer:
`\cos(2\theta)=(119)/(169)`

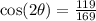
Explanation:

There are a set of identities known as the double angle identities (named as such because you are doubling the angle). For cosine, the following relationships hold true:

`\cos(2\theta)=\cos^2(\theta)-\sin^2(\theta)=1-2\sin^2(\theta)=2\cos^2(\theta)-1`

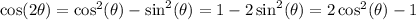
We are given the sine relationship and from the above identity, we can use the middle identity in order to solve for the cosine.

`\cos(2\theta)=1-2\sin^2(\theta)=1-2((5)/(13))^2=1-2((25)/(169))=1-(50)/(169)=(119)/(169)`

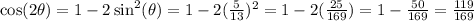
So your answer is 119/169.

Alternatively, you could've solved for the other side using the Pythagorean Theorem and created a cosine relationship for that. However, I think the method I have used is the easiest given the information.