Answer:
(a) It increases by 8
(b) It stays the same
Step-by-step explanation:
First, we need to calculate the mean and median of the original data. This data is
335, 393, 425, 453, 489, 542, 556, 563, 623, 661
Then, the mean is the sum of all the values divided by the number of values, so

The median is the value that divides the set into two sets of equal sizes. In this case, these numbers are 489 and 542 because there are 4 numbers before 489 and 4 numbers after 542
335, 393, 425, 453, 489, 542, 556, 563, 623, 661
Then, the median is
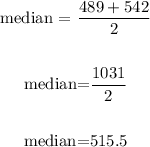
Now, we need to calculate the mean and median when 335 is changed to 415. So, the new data set is
393, 415, 425, 453, 489, 542, 556, 563, 623, 661
Then, the mean is

And the median is 515.5 because the numbers in the middle are the 489 and 542
393, 415, 425, 453, 489, 542, 556, 563, 623, 661
Therefore, we can say that:
The mean increased by 8 because 512 - 504 = 8
The median stays the same
So, the answers are
(a) It increases by 8
(b) It stays the same