Question

The size of a population of bacteria is modeledby the function P, where P(t) gives thenumber of bacteria and t gives the number ofhours after midnight for 0 < t < 10. Thegraph of the function P and the line tangent toP at t= 8 are shown above. Which of thefollowing gives the best estimate for theinstantaneous rate of change of P at t = 8?

Answer 1

Answer: The graph of the P(t) has been provided, we have to find the instantaneous slope of P(t) at t = 8:

`Slope=m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)`

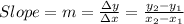
Therefore we need two y values and two x values, which can be obtained as follows:

`\begin{gathered} t=8 \\ \\ \therefore\Rightarrow \\ \\ x_1=t_1=8-0.1=7.9 \\ \\ y_1=P(t_1)=P(7.9) \\ \\ x_2=t_2=8+0.1=8.1 \\ \\ y_2=P(t_2)=P(8.1) \\ \\ \therefore\rightarrow \\ \\ Slope=(P(8.1)-P(7.9))/(t_2-t_1)\rightarrow(1) \\ \end{gathered}`

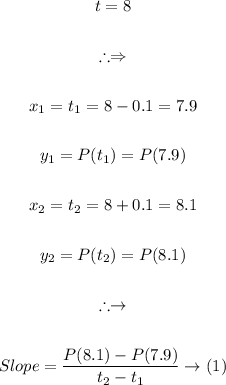
Equation (1) corresponds to the third, option, therefore that is the answer.