Question

Polynomials

(7n^4-14 - 5n^3) (7-8n^3 + 11n^4)​

Answer 1

`\boxed{22n^8-16n^7-140n^4+112n^3-98}`

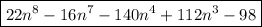
Explanation:

`(7n^4-14 - 5n^3) (7-8n^3 + 11n^4)`

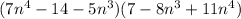
According to the distributive property, each term multiplies each of the terms in the other equation. Therefore, we can do the following:

`\begin{aligned}\Rightarrow &7n^4 (7-8n^3 + 11n^4)= 49n^4-56n^3 n^4+77n^4n^4 \\&=49n^4-56n^7+77n^8 \end{aligned}`

`\begin{aligned}\Rightarrow &-14 (7-8n^3 + 11n^4)\\& = -98+112n^3-154n^4 \end{aligned}`

`\begin{aligned}\Rightarrow &-5n^4 (7-8n^3 + 11n^4)= -35n^4+40n^3n^4-55n^4n^4 \\&=-35n^4+40n^7-55n^8 \end{aligned}`

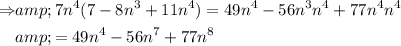
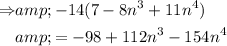
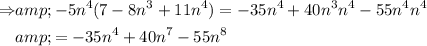
Next, we combine all the terms of the plynomial equation:

`49n^4-56^7+77n^8-98+112n^3-154n^4-35n^4+40n^7-55n^8`

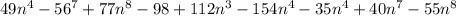
common factor:

`22n^8-16n^7-140n^4+112n^3-98`

By this, we have solved the exercise.

`\text{-B$\mathfrak{randon}$VN}`