To reflect the given matrix over the x-axis, you have to multiply both matrices:
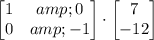
Multiply each term of the first row of the first matrix with the corresponding terms of the column of the second matrix and add the results:
Repeat the process for the second row of the first matrix
The resulting matrix is:
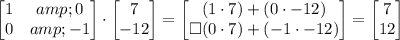
The correct option is option D.