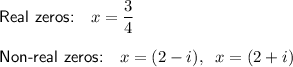Question

One zero is (2-i). Find all zeros real and nonreal

Answer 1

To find:-

• All zeroes of f(x) = 4x³ - 19x² + 32x - 15 , if one zero is (2-i) .

Answer:-

We are here given that one zero of a cubic polynomial is ( 2 - i ) . So the other conjugate root will be , ( 2 + i ) as one of the root is a complex number .

So , if (2 - i) and (2 + i) are the zeroes of f(x) , then ;

`\implies x - (2+i ) = x - 2-i \\`

and,

`\implies x -(2-i) = x -2 + i \\`

will be a factor of f(x) , now we can find the product of these factors as ,

`\implies g(x)= (x-2+i)(x-2-i) \\`

`\implies g(x) = \{ (x-2) + i \} \{ (x-2)-i\})\\`

solve using the identity ,
`a^2-b^2 = (a+b)(a-b)`

`\implies g(x) = (x-2)^2 - (i)^2 \\`

`\implies g(x) = x^2 - 4x + 4 - (√(-1))^2 \\`

`\implies g(x) = x^2 -4x + 4 -(- 1 ) \\`

`\implies g(x) = x^2 -4x + 5\\`

This means
`g(x) = x^2-4x + 5` will be a factor of f(x) , now we may divide f(x) by g(x) as , ( see attachment)

From division , we get the other factor as
`4x-3` . To find out the zero , equate it with 0 as ,

`\implies 4x - 3 = 0 \\`

`\implies 4x = 3 \\`

`\implies \underline{\underline{\quad x =(3)/(4)\quad }} \\`

Hence the other two zeroes are (2+i) and 3/4 .

and we are done!

Answer 2

`\textsf{Real zeros:}\quad x=(3)/(4)\\\\\textsf{Non-real zeros:}\quad x=(2-i),\;\;x=(2+i)`

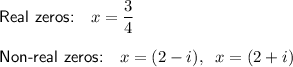
Explanation:

The zeros of a function f(x) are the x-values where f(x)=0.

Given information:

• Cubic polynomial function with real coefficients.
• Zeros: (2 - i)
• Leading coefficient: 4.

For any complex number
`z=a+bi`, the complex conjugate of the number is defined as
`z^*=a-bi`.

If f(z) is a polynomial with real coefficients, and z₁ is a root of f(z)=0, then its complex conjugate z₁* is also a root of f(z)=0.

Therefore, if f(x) is a polynomial with real coefficients, and (2 - i) is a root of f(x)=0, then its complex conjugate (2 + i) is also a root of f(x)=0.

According to the Factor Theorem, if f(x) is a polynomial and f(r)=0, then (x – r) is a factor of f(x).

Therefore, two factors of the given function are:

• (x - (2 - i))

• (x - (2 + i))

As the polynomial is cubic (highest exponent is 3), and the leading coefficient is 4, the polynomial in factored form is:

`f(x)=4(x-r)(x-(2-i))(x-(2+i))`

Expand the polynomial:

`f(x)=4(x-r)(x-2+i)(x-2-i)`

`f(x)=4(x-r)(x^2-2x-ix-2x+4+2i+ix-2i-i^2)`

`f(x)=4(x-r)(x^2-4x+4-i^2)`

`f(x)=4(x-r)(x^2-4x+4-(-1))`

`f(x)=4(x-r)(x^2-4x+5)`

`f(x)=4(x^3-4x^2+5x-rx^2+4rx-5r)`

`f(x)=4x^3-16x^2+20x-4rx^2+16rx-20r`

`f(x)=4x^3-(16+4r)x^2+(20+16r)x-20r`

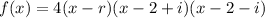
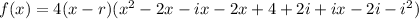
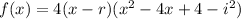
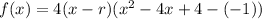
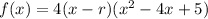
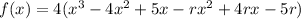
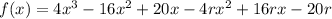
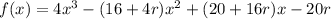
Compare the coefficients of the terms in x of the original function and the expanded factored function to find the third zero, r:

`\implies 20+16r=32`

`\implies 16r=12`

`\implies r=(12)/(16)`

`\implies r=(3)/(4)`

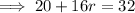
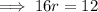
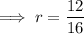
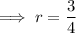
Check the value of r by comparing the coefficients of the terms in x²:

`\implies -(16+4r)=-19`

`\implies 16+4r=19`

`\implies 4r=3`

`\implies r=(3)/(4)`

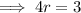
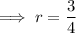
Therefore, the zeros of the given polynomial are:

`\textsf{Real zeros:}\quad x=(3)/(4)\\\\\textsf{Non-real zeros:}\quad x=(2-i),\;\;x=(2+i)`