Question

Hiru Tare | (If A + B + C = π and sin A = sin B sin C prove that): cot B + cot C = 1​

Answer 1

`\textsf{If\;\;$A + B + C = \pi$\;\;and\;\;$\sin A = \sin B\sin C$,\;\;then\;\;$\cot B + \cot C = 1$.}`

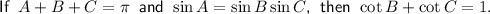
Explanation:

We are given that:

`\textsf{Equation 1:} \quad A + B + C = \pi`

`\textsf{Equation 2:} \quad \sin A = \sin B \sin C`

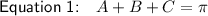
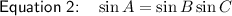
We need to prove that:

`\cot B + \cot C = 1`

Begin by rearranging the first equation to isolate (π - A):

`\implies \pi-A=B+C`

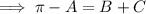
Use this and the identity sin(A) = sin(π - A) to rewrite sin(A) in terms of B and C:

`\implies \sin A=\sin(\pi - A)`

`\implies \sin A=\sin(B+C)`

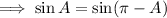
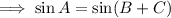
Expand sin(B + C) using the identity sin(x + y) = sin(x)cos(y) + cos(x)sin(y):

`\implies \sin A=\sin(B+C)`

`\implies \sin A=\sin B \cos C +\cos B \sin C`

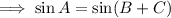
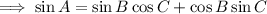
Given that sin(A) = sin(B)sin(C), substitute the two equations for sin(A) to create an equation in B and C only:

`\implies \sin B \cos C + \cos B\sin C=\sin B \sin C`

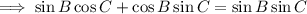
Divide both sides of the equation by sin(B)sin(C):

`\implies (\sin B \cos C + \cos B \sin C)/(\sin B \sin C)=(\sin B \sin C)/(\sin B \sin C)`

`\implies (\sin B \cos C)/(\sin B \sin C) + (\cos B \sin C)/(\sin B \sin C)=1`

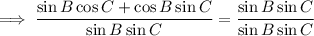
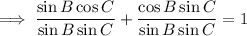
Cancel the common factors:

`\implies (\cos C)/( \sin C) + ( \cos B)/(\sin B)=1`

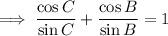
Use the identity cos(x)/sin(x) = cot(x):

`\implies \cot C +\cot B=1`

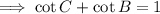
Rearrange the terms on the left side of the equation:

`\implies \cot B+ \cot C=1`

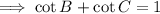
Therefore, we have proved that cot(B) + cot(C) = 1, given that A + B + C = π and sin(A) = sin(B)sin(C).