Question

How many pounds of candy that sells for $0.87 per lb must be mixed with candy that sells for $1.22 per lb to obtain 9 lb of a mixture that should sell for $0.91 per lb?$0.87-per-lb candy: _____lb$1.22-per-lb candy: _____lb(Type an integer or decimal rounded to two decimal places as needed.)

Answer 1

Let x and y be the candy pounds that sells for $0.87 and $1.22 , respectively. Since they both must add up to 9 lb, we have

`x+y=9...(A)`

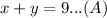
On the other hand, the mixture should sell for $0.91 per lib, so we can write,

`0.87x+1.22y=9*0.91`

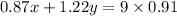
Or euivalently,

`\begin{gathered} (0.87)/(0.91)x+(1.22)/(0.91)y=9 \\ that\text{ is, } \\ 0.95604x+1.340659y=9...(B) \end{gathered}`

Then, we need to solve the following system of equations:

`\begin{gathered} x+y=9...(A) \\ 0.95604x+1.340659y=9 \end{gathered}`

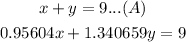
Solving by elimination method.

In order to eliminate variable x, we can to multiply equation (A) by -0.95604 and get an equivalent system of equations:

`\begin{gathered} -0.95604x-0.95604y=-8.60439 \\ 0.95604x+1.340659y=9 \end{gathered}`

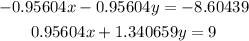
Then, by adding both equations, we get

`0.384619y=0.39561`

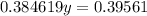
Then, y is given by

`\begin{gathered} y=(0.39561)/(0.384619) \\ y=1.02857 \end{gathered}`

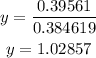
Once we have obtained the result for y, we can substitute in into equation (A), that is,

`x+1.02857=9`

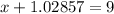
then, x is given as

`\begin{gathered} x=9-1.02857 \\ x=7.9714 \end{gathered}`

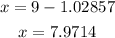
Therefore, by rounding to two decimal places, the answer is:

$ 0.87 per lb of candy: 7.97 lb

$1.22-per-lb of candy: 1.03 lb