Question

`solve for x; ln4x-3ln(x^2)=ln2`

Answer 1

`x=\sqrt[5]{2}`

Explanation:

We are given the natural logarithmic equation:

`\ln 4x - 3 \ln (x^2) = \ln 2`

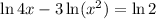
To solve for x, use the logarithm laws to isolate x on one side of the equation.

`\textsf{Apply the power law:} \quad n \ln x=\ln x^n`

`\implies \ln 4x - \ln (x^2)^3 = \ln 2`

`\textsf{Apply the exponent rule:} \quad (a^b)^c=a^(bc)`

`\implies \ln 4x - \ln x^6 = \ln 2`

`\textsf{Apply the quotient law:} \quad \ln x - \ln y=\ln \left((x)/(y)\right)`

`\implies \ln \left((4x)/(x^6)\right) = \ln 2`

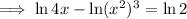
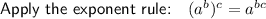
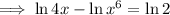
Factor out the common term x:

`\implies \ln \left((4)/(x^5)\right) = \ln 2`

`\textsf{Apply the equality law:} \quad \textsf{If $\ln x= \ln y$ then $x=y$}`

`\implies (4)/(x^5) = 2`

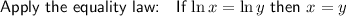
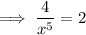
Multiply both sides by x⁵:

`\implies 4= 2x^5`

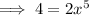
Divide both sides by 2:

`\implies x^5=2`

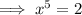
Take the 5th root of both sides:

`\implies x=\sqrt[5]{2}`