Question

Find the area of the shaded region of the cardioid r=9−9cos(0).

Answer 1

The area of the shaded region of the cardioid
`r=9-9 \cos (\theta)` is
`(243 \pi-648)/(8)`

Here the shaded region is from
`\theta=0` to
`\theta=(\pi)/(2)`

Thus, the integral setup for the area is given as:

`\begin{aligned}\text { Area } & =\int_0^{(\pi)/(2)} (r^2)/(2) d \theta \\& =\int_0^{(\pi)/(2)} ((9-9 \cos (\theta))^2)/(2) d \theta \\& =(1)/(2) \cdot \int_0^{(\pi)/(2)} 81-162 \cos (\theta)+81 \cos ^2(\theta) d \theta \\& =(1)/(2)\left(\int_0^{(\pi)/(2)} 81 d \theta-\int_0^{(\pi)/(2)} 162 \cos (\theta) d \theta+\int_0^{(\pi)/(2)} 81 \cos ^2(\theta) d \theta\right) \\\end{aligned}`

`\begin{aligned}& =(1)/(2)\left([81 \theta]_0^{(\pi)/(2)}-162[\sin (\theta)]_0^{(\pi)/(2)}+(81)/(2)\left(\int_0^{(\pi)/(2)} 1 d \theta+\int_0^{(\pi)/(2)} \cos (2 \theta) d \theta\right)\right) \\& =(1)/(2)\left([81 \theta]_0^{(\pi)/(2)}-162[\sin (\theta)]_0^{(\pi)/(2)}+(81)/(2)\left([\theta]_0^{(\pi)/(2)}+[\sin (2 \theta)]_0^{(\pi)/(2)} (1)/(2)\right)\right) \\\end{aligned}`

`\begin{aligned}& =(1)/(2)\left((81 \pi)/(2)-162+(81 \pi)/(4)\right) \\& =(243 \pi-648)/(8)\end{aligned}`

Thus, the required area is
`(243 \pi-648)/(8)`

Answer 2

The calculated area of the shaded region is 243/2π

Finding the area of the shaded region

From the question, we have the following parameters that can be used in our computation:

r = 9 - 9cos(θ)

The area is calculated using

`\text{Area} = \frac12\int\limits^(2\pi)_0 {r^2} \, d\theta`

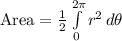
Substitute the known values into the equation

`\text{Area} = \frac12\int\limits^(2\pi)_0 {(9 - 9\cos(\theta))^2} \, d\theta`

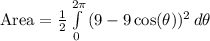
Expand

`\text{Area} = \frac12\int\limits^(2\pi)_0 {(81 - 182 \cos(\theta) + 81 \cos^2(\theta))} \, d\theta`

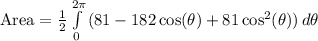
Integrate

`\text{Area} = -\frac12 * \frac{81\sin\left(2{\theta}\right)-728\sin\left({\theta}\right)+486{\theta}}{4}|\limits^(2\pi)_0`

`\text{Area} = - \frac{81\sin\left(2{\theta}\right)-728\sin\left({\theta}\right)+486{\theta}}{8}|\limits^(2\pi)_0`

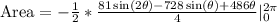
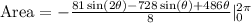
Expand

`\text{Area} = - \frac{81\sin\left(2 * 2{\pi}\right)-728\sin\left({2\pi}\right)+486 * {2\pi}}{8} + \frac{81\sin\left(2*0{}\right)-728\sin\left({0}\right)+486*0}{8}`

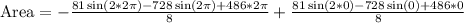
Evaluate

Area = 243/2π

Hence, the area of the shaded region is 243/2π