Question

PLEASE HELP ME‼️(IMAGE ATTACHED)

Solve the system of equations using determinants.

3x + 2y = 7

3x - y = -8

Find the values of determinants D, Dx and Dy

D=?
Dx=?
Dy=?

Answer 1

• (x, y) = (-1, 5)
• D = -9
• Dx = 9
• Dy = -45

Explanation:

You want to solve the system of equations using determinants:

• 3x +2y = 7
• 3x -y = -8

Determinants

The determinant of a 2×2 matrix is the difference between the product of the diagonal terms and the product of the off-diagonal terms:

`\left|\begin{array}{cc}a&b\\c&d\end{array}\right|=ad-cb`

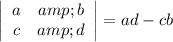
Solution using determinants

Cramer's Rule tells you the solution to a system of linear equations can be found from the determinants obtained for the matrix of coefficients, and for the matrices created by replacing successive columns of the coefficient matrix by the constant vector on the right of the equal sign.

The attached calculator display shows these three matrices and their determinants.

D = 3(-1) -3(2) = -9

Dx = 7(-1) -(-8)(2) = 9

Dy = 3(-8) -3(7) = -45

The solutions using these values are ...

x = Dx/D = 9/(-9) = -1

y = Dy/D = -45/(-9) = 5

The solution using determinants is (x, y) = (-1, 5).

__

Additional comment

If D=0, the system is either dependent or inconsistent, and there is no single solution.