Question

I'm soooooo confuzzledddjskdnsk???????? :)
​

Answer 1

a) n = 2

b) r = 50, s = 25

c) t = 6, u = 8

Explanation:

Part a)

`\textsf{The exact value of $\cos 30^(\circ)$\;is\;$(√(3))/(2)$.}`

`\textsf{Therefore,\;if\;$\cos 30^(\circ)=(√(3))/(n)$,\;then\;$n=2$.}`

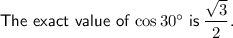
Part b)

If we draw a line segment between points A and C, we create triangle ABC and can then use the cosine rule to calculate the length of AC².

`\boxed{\begin{minipage}{7 cm}\underline{Cosine Rule} \\\\$c^2=a^2+b^2-2ab \cos C$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides of the triangle.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}`

From inspection of triangle ABC:

• a = BA = 5 cm
• b = BC = 5 cm
• c = AC
• C = ∠ABC = 30°

Substitute the values into the cosine rule formula:

`\begin{aligned}\implies AC^2&=BA^2+BC^2-2(BA)(BC)\cos 30^(\circ)\\&=5^2+5^2-2(5)(5) \cos 30^(\circ)\\&=25+25-50 \cos 30^(\circ)\\&=50-50 \cos 30^(\circ)\\ \end{aligned}`

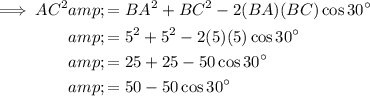
Substitute the value of cos 30° from part a).

`\begin{aligned}\implies AC^2&=50-50 \cos 30^(\circ)\\&=50-50 \cdot (√(3))/(2)\\&=50-25√(3) \end{aligned}`

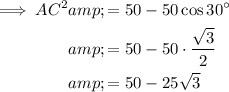
Therefore, if r - s√3 = 50 - 25√3 then:

• r = 50
• s = 25

Part c)

If we draw a line segment between points P and Q, we create triangle PBQ.

As line segment
`\sf A\;\!F` is parallel to line segment CD, and BP = BQ = 10cm, then line segment PQ is parallel to and equal in length to line segment AC. Therefore:

• PQ² = AC² = (50 - 25√3) cm

Again, use the cosine rule to calculate cos PBQ, but this time use the rearranged equation to find the angle.

`\boxed{\begin{minipage}{7.6 cm}\underline{Cosine Rule (for finding angles)} \\\\$\cos(C)=(a^2+b^2-c^2)/(2ab)$\\\\\\where:\\ \phantom{ww}$\bullet$ $C$ is the angle. \\ \phantom{ww}$\bullet$ $a$ and $b$ are the sides adjacent the angle. \\ \phantom{ww}$\bullet$ $c$ is the side opposite the angle.\\\end{minipage}}`

From inspection of triangle PBQ:

• a = BP = 10 cm
• b = BQ = 10 cm
• c² = PQ² = (50 - 25√3) cm
• C = ∠PBQ

Substitute the values into the cosine rule formula:

`\begin{aligned}\implies \cos PBQ&=(BP^2+BQ^2-PQ^2)/(2(BP)(BQ))\\\\&=(10^2+10^2-(50 - 25√(3)))/(2(10)(10))\\\\&=(200-50 + 25√(3))/(2(10)(10))\\\\&=(150 + 25√(3))/(200)\\\\&=(6+√(3))/(8)\end{aligned}`

Therefore, the values of t and u are:

• t = 6
• u = 8