Answer:
The interest rate (to the nearest percent) is 10%.
Explanation:
The formula to calculate compound interest is:
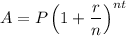
where:
- A = Final amount.
- P = Principal amount.
- r = Interest rate (in decimal form).
- n = Number of times interest is applied per year.
- t = Time (in years).
Given values:
- A = $8000
- P = $5000
- n = 1 (annually)
- t = 5 years
Substitute the values into the formula and solve for r:
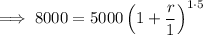
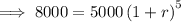
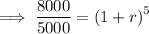
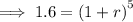
![\implies \sqrt[5]{1.6}=\sqrt[5]{\left(1+r\right)^(5)}](https://img.qammunity.org/2024/formulas/mathematics/high-school/ifmd3dx97zj4wgon0cylif9de0hwj5ninm.png)
![\implies \sqrt[5]{1.6}=1+r](https://img.qammunity.org/2024/formulas/mathematics/high-school/48ze28vilusefn4xcgyex55n5phtoewi4y.png)
![\implies r=\sqrt[5]{1.6}-1](https://img.qammunity.org/2024/formulas/mathematics/high-school/ir5oduijdf7iti2awff0xre8itnvb3yrtz.png)
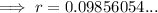
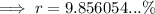
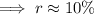
Therefore, the interest rate (to the nearest percent) is 10%.