Question

State the domain and the range of
`f(x)=√(-x+4) +2`

Answer 1

Domain: (-∞, 4]

Range: [2, ∞)

Explanation:

Domain

The domain of a function is the set of all possible input values (x-values).

The square root of a negative number cannot be taken.

Therefore, to find the domain, set the expression under the square root of the given function to greater than or equal to zero and solve for x:

`\implies -x+4\geq0`

`\implies -x+4-4\geq0-4`

`\implies -x\geq-4`

`\implies (-x)/(-1)\geq(-4)/(-1)`

`\implies x\leq4`

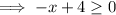
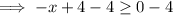
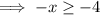
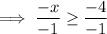
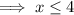
(When dividing by 1 negative number, remember to reverse the inequality sign).

Therefore, the domain of the function is:

• Solution: x ≤ 4
• Interval notation: (-∞, 4]

Range

The range of a function is the set of all possible output values (y-values).

As the domain of the function is restricted to (-∞, 4], this means the range is also restricted.

As the expression under the square root is greater than or equal to zero, the range will be 2 more than this.

Therefore, the range of the function is:

• Solution: f(x) ≥ 2
• Interval notation: [2, ∞)