Answer:
WR ≈ 13.862
Explanation:
using Pythagoras' identity in the right triangle.
the square on the hypotenuse is equal to the sum of the squares on the other 2 sides , that is
WR² + RT² = WT²
WR² + 12.1² = 18.4²
WR² + 146.41 = 338.56 ( subtract 146.41 from both sides )
WR² = 192.15 ( take the square root of both sides )
WR =
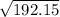 ≈ 13.862 ( to the nearest thousandth )
≈ 13.862 ( to the nearest thousandth )