Question

What is the 10th term of the following sequence?

16, -8, 4, -2, …
show all steps please

Answer 1

To find:-

• 10th term of the geometric sequence.

Answer:-

The given geometric sequence to us is ,

16 , - 8 , 4 , - 2 . . . . .

In a geometric sequence each term is multiplied by a number to obtain the next term.

Now let's find the common ratio (r) , to find the common ratio divide a term by its preceding term as ,

`\implies r = (-8)/(16)\\`

`\implies r =(-1)/(2)\\`

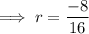
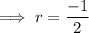
Hence the common ratio is -1/2 .

Now to find the nth term of a GP , we can use the formula, which is;

`\implies T_n = ar^(n-1) \\`

where,

• 
  `T_n` is the nth term.
• 
  `a` is the first term = 16
• 
  `r` is the common ratio = -1/2
• 
  `n` is number of the term = 10

So on substituting the respective values, we have;

`\implies T_(10) = 16 \bigg( (-1)/(2)\bigg)^(10-1)\\`

`\implies T_(10) = 2^4 \bigg( (-1)/(2)\bigg)^9\\`

`\implies T_(10)= -1\bigg( (2^4)/(2^9)\bigg) \\`

`\implies T_(10)=-1\bigg((1)/(2^5)\bigg) \\`

`\implies \underline{\underline{\green{{T_(10)=-(1)/(32)}}}} \\`

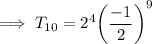
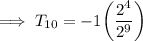
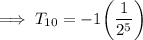
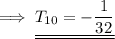
Hence the tenth term is -1/32 .

and we are done!

Answer 2

10th term = -1/32 or -0.03125

Explanation:

This is a geometric sequence with a common ratio of -1/2:

r = -1/2

We can use the formula for the nth term of a geometric sequence to find the nth term:

an = a1 * r^(n-1)

where:

a1 = first term = 16

n = the index of the term we want to find

Substituting the values, we get:

an = 16 * (-1/2)^(n-1)

Therefore, the nth term of the sequence is given by the formula:

an = 16 * (-1/2)^(n-1).

For 10 th term

we need to substitute 10 in place of n.

so

a_10=16*(-1/2)^(10-1)=-1/32=-0.03125