Question

What is the solution to the inequality |2x + 3| < 7?

Answer's
4 < x < 10
–5 < x < 2
x < 4 or x > 10
x < –5 or x > 2

Answer 1

The solution to the inequality |2x + 3| < 7 is:

• -5 < x < 2

Explanation:

The given inequality contains an absolute value.

The absolute value of an expression is its positive numerical value.

Step 1

To solve the absolute value inequality, begin by isolating the absolute value on one side of the equation. (This has already been done for us).

`\implies |2x+3| < 7`

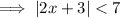
Step 2

Apply the absolute rule:

`\boxed{\textsfu}`

Therefore, we can create two inequalities:

`\textsf{Inequality 1:} \quad 2x+3 < 7`

`\textsf{Inequality 2:} \quad 2x+3 > -7`

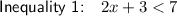
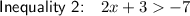
Step 3

Solve both inequalities:

`\boxed{\begin{aligned}\underline{\sf Inequality\;1}\\ \implies 2x+3& < 7\\2x& < 4\\x& < 2\end{aligned}}`
`\boxed{\begin{aligned}\underline{\sf Inequality\;2}\\ \implies 2x+3& > -7\\2x& > -10\\x& > -5\end{aligned}}`

Step 4

Finally, merge the overlapping intervals:

`-5 < x < 2`

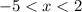
Solution

The solution to the inequality |2x + 3| < 7 is -5 < x < 2.