Answer:
Domain:
 or in interval notation
or in interval notation
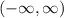
Range:
 or in interval notation
or in interval notation

Explanation:
We are given
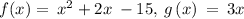
To find
 :
:
Substitute 3x wherever there is an x term in f(x)
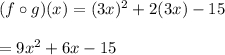
There is no restriction on the value of x so x is the set of all real numbers which means -∞ < x < ∞
 in interval notation
in interval notation
To find the range, note that the equation
 is the equation of a parabola
is the equation of a parabola
The general parabola equation in polynomial form is
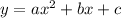
Comparing

we see
a = 9
b = 6
c = -15
The vertex of this parabola is either minimum or maximum depending on the value of a
If a > 0 then it is a upward facing parabola and the vertex is a minimum
If a < 0 then it is a downward facing parabola and the vertex is a maximum
Since a = 9 > 0 it is a upward facing parabola and the vertex is a minimum
The x-coordinate of the vertex is given by

The y-coordinate of the vertex can be found by plugging in this value of x into the equation
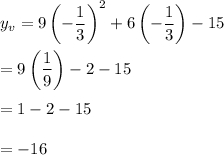
This would be the minimum value of f(x). There is no limit to the upper value of f(x) so the range is given by [-16, ∞)
Range of
 or
or

In interval notation this would be
[-16, ∞ )