Question

#19 i

Write the quadratic function in vertex form. Then identify the vertex.
f(x)=x²-8x + 19

Pls help me

Answer 1

Vertex form: f(x) = (x - 4)² + 3

Vertex: (4, 3)

Explanation:

Use completing the square to convert the equation into vertex form.

Remember that the value of the equation must stay the same, so anything added when creating the square polynomial should also be subtracted.

f(x) = x² - 8x + 19

= (x² - 8x + 16) + 19 - 16

= (x-4)² + 3

Vertex form is y = a(x - h)²+k

a represents the scalar, in this case the scalar is 1.

Pull the coordinate (h, k) from the equation.

The vertex is (4, 3).

Answer 2

To find:-

• To write the quadratic function in vertex form and then identify the vertex.

Answer:-

The given quadratic function to us is ,

`\implies f(x) = x^2-8x+19`

In order to find the vertex form, we need to complete the square for the quadratic function.

`\implies f(x) = x^2 - 8x +19`

`\implies f(x) = (x^2 -8x + 16 ) + 19 -16`

`\implies f(x) =\{ (x^2-2(4)(x) + 4^2) \}+ 3`

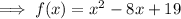
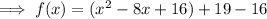
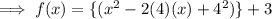
Now we can see that the expression inside the curly brackets are in the form of
`a^2-2ab+b^2` , which is the whole square of
`a+b` . So we can rewrite it as ,

`\implies f(x) = ( x-4)^2 + 3`

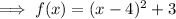
Now the standard equation of vertex form is ,

`\implies f(x) = a(x-h)^2 + k`

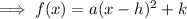
where ,

• (h,k) is the vertex.

So on comparing with respect to the standard form, we have,

`\implies h = 4`

`\implies k = 3`

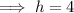
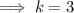
Henceforth, the vertex would be ,

`\implies\underline{\underline{\green{\text{ Vertex = ( 4 , 3 ) }}}}`

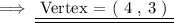
Hence the vertex of the function is (4,3) .

and we are done!