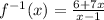Question

Select the correct choice and fill in the blank if necessary

Answer 1

Given

`f(x)=(x+6)/(x-7)`

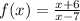
Recall

The horizontal line test can be used to determine if a function is one-to-one given a graph. Simply superimpose a horizontal line onto a graph and see if it intersects the graph at more than one point. If it does, the graph is not one-to-one and if it only intersects at one point, it will be one-to-one.

The graph

It passed the horizontal line test, therefore is one to one function

Part B

`f(x)=(x+6)/(x-7)`

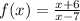
Step 1

Replace f(x) with y

`y=(x+6)/(x-7)`

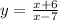
Step 2

Inter change y and x

`x=(y+6)/(y-7)`

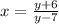
Step 3

Make y the subject

`\begin{gathered} x=(y+6)/(y-7) \\ x(y-7)=y+6 \\ xy-7x=y+6 \\ xy-y=6+7x \\ y(x-1)=6+7x \\ divide\text{ both sides by x-1} \\ y=(6+7x)/(x-1) \end{gathered}`

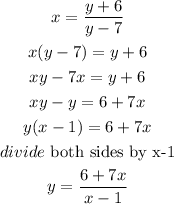
Step 4

Replace y with f^-1

`f^(-1)(x)=(6+7x)/(x-1)`

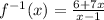
The final answer

`f^(-1)(x)=(6+7x)/(x-1)`