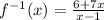Given
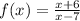
Recall
The horizontal line test can be used to determine if a function is one-to-one given a graph. Simply superimpose a horizontal line onto a graph and see if it intersects the graph at more than one point. If it does, the graph is not one-to-one and if it only intersects at one point, it will be one-to-one.
The graph
It passed the horizontal line test, therefore is one to one function
Part B
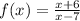
Step 1
Replace f(x) with y
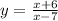
Step 2
Inter change y and x
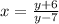
Step 3
Make y the subject
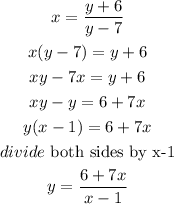
Step 4
Replace y with f^-1
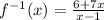
The final answer