Answer:
The graph falls to the left and rises to the right.
Explanation:
Given f(x) defined below:
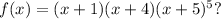
We are to determine the end behavior of the polynomial using the Leading Coefficient Test.
When using the Leading coefficient test, the following rule applies:
• When the ,degree is odd, and the ,leading coefficient is positive,, the graph falls to the left and rises to the right.
,
• When the ,degree is odd, and the ,leading coefficient is negative,, the graph rises to the left and falls to the right.
,
• When the ,degree is even, and the ,leading coefficient is positive,, the graph rises to the left and right.
,
• When the ,degree is even, and the ,leading coefficient is negative,, the graph falls to the left and right.
Back to our function, f(x):
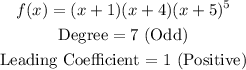
From the first rule above, we can conclude that the graph falls to the left and rises to the right.
A graph of f(x) is attached which confirms this end behavior.