Question

Solve the right triangle with a= 1.42 and b=17.1 . Round off the results according to the table below

Answer 1

A)

Step-by-step explanation

Step-by-step explanation

Step 1

c) to find the measure of the hypotenuse we can use the Pythagorean theorem, it states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)

Step 1

a) Let

`\begin{gathered} a=1.42 \\ b=17.1 \end{gathered}`

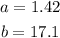
b) now, replace and solve for c

`\begin{gathered} a^2+b^2=c^2 \\ 1.42^2+17.1^2=c^2 \\ 294.4264=c^2 \\ c=√(294.4264) \\ c=17.15885 \\ rounded \\ c=17.159 \end{gathered}`

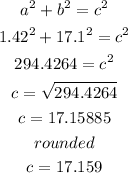
Step 2

angle A

to solve for angle A we can use tan function, so

`tan\theta=\frac{opposite\text{ side}}{adjacent\text{ side}}`

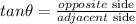
replace

`\begin{gathered} tan\text{ A=}(a)/(b) \\ tanA=(1.42)/(17.1) \\ A=\tan^(-1)((1.42)/(17.1)) \\ A=4.747\text{ \degree} \end{gathered}`

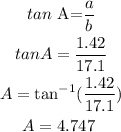
Step 3

for angle B we can use tan function

let

`\begin{gathered} opposit\text{ side=b} \\ adjacent\text{ side=a} \end{gathered}`

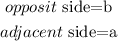
replace and solve for angle B

`\begin{gathered} tan\text{ B=}(b)/(a) \\ tanB=(17.1)/(1.42) \\ B=\tan^(-1)((17.1)/(1.42)) \\ B=85.252\text{ \degree} \\ \end{gathered}`

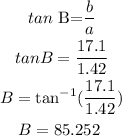
I hope this helps you