Question

The length of two equal sides of an isosceles triangle is 2x + 3. The length of the third side is 2x. Its perimeter is 36 centimeters. Write an equation that could be used to find the value of x. Solve for x and then find the length of all three sides.

Answer 1

To find:-

• To write an equation that can be used to solve for x .
• The sides of the triangle using the equation.

Answer:-

For finding the perimeter of a any figure, we simply find the sum of its side lengths. So for a triangle it will be the sum of it three sides. And according to the question two sides are
`2x+3` and one side is
`2x` . So we can find the perimeter as ;

`\implies s_1 + s_2 + s_3 \\`

and here,

• 
  `s_1` =
  `s_2` = 2x + 3
• 
  `s_3 = 2x`

`\implies 2x + 3 + 2x + 3 + 2x \\`

`\implies 6x + 6 \\`

But it's given that the perimeter is 36cm. So they must be equal . Hence we can equate them as ,

`\implies 6x + 6 = 36 \\`

So the required equation is ,

`\implies \underline{\underline{\green{ 6x + 6 = 36 }}}`

Solve out for x now as ,

`\implies 6( x + 1 ) = 36 \\`

`\implies x + 1 = (36)/(6)\\`

`\implies x+1 = 6\\`

`\implies x = 6-1 \\`

`\implies x = 5 \\`

Hence the value of x is 5 .

Now in order to find out the side lengths substitute
`x=5` in the expression for the side lengths as,

`\implies s_1 = s_2 = 2x + 3 =\{ 2 (5)+3\} \ cm = \boxed{13\ cm } \\`

`\implies s_2 = 2x = 2(5cm) = \boxed{10cm} \\`

Hence the side lengths are 13cm , 13cm and 10cm .

and we are done!

Answer 2

The value of x = 5.

The length of all three sides is 13 cm, 13 cm and 10 cm.

Explanation:

The perimeter of a two-dimensional shape is the distance all the way around the outside. Therefore, the perimeter of a triangle is the sum of its side lengths.

Given the lengths of the two equal sides of the triangle are (2x + 3) and the length of the third side is 2x, the equation for the perimeter is:

`\begin{aligned}\implies \textsf{P} &= 2(2x + 3) + 2x\\&=4x+6+2x\\&=6x+6\end{aligned}`

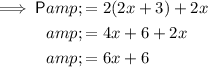
Given the perimeter is 36 cm, substitute P = 36 into the equation and solve for x:

`\begin{aligned} 6x+6&=36 \\6x+6-6&=36-6\\6x&=30\\(6x)/(6)&=(30)/(6)\\x&=5\end{aligned}`

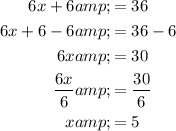
Therefore, the value of x = 5.

To find the length of all three sides, substitute x = 5 into the given expressions.

Equal sides

`\begin{aligned} \implies 2(5)+3&=10+3\\&=13\; \sf cm\end{aligned}`

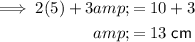
Third side

`\implies 2(5)=10\; \sf cm`

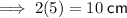
Therefore, the length of all three sides is 13 cm, 13 cm and 10 cm.