Question

Please help my brain is mush i dont understand how this works nd i still have 11 assignments after this-

1. Do these graphs represent functions? Explain.
2. Choose one value that is the domain of both y(x)=x^2 and y^2=x and that is greater that 0. Substitute that value into y(x)=x^2 and y^2=x and then simplify. explain how your answers help show that graph on the left represents a function while the graph on the right represents a relation. show your work and use function notation where possible.

Answer 1

See step by step

Explanation:

1. First question, do they represent functions? The one o. the left is a function because if you do the vertical line test. It only passes through a point once so it is a function. while on the right if you do the vertical line test, it passes through a point twice so it not a function. For 2.. n other words, since the domain of this equation is all real numbers or negative infinity to positives infinity

let say x=1 and x=-1 and we use the equation

`y = {x}^(2)`

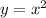
when we plug both those in we get

`y = 1`

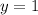
this means that we can have two different x-values to equal out to the same y value. This is the definition of a function. So the one on the right is a function.

However the one on the left is a relation. TO Prove it, the domain of that function is all real numbers equal to or greater than zero, so let use 4.

`{y}^(2) = 4`

`{y} = 2 \: or \: - 2`

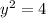
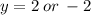
Since there are 2 possible answer choices as the y value, this isn't a function. It a relation. It maps a group of ordered sets to one x value. Which is the opposite of the function. So the one of the left is a relation