Question

Match each of the equations with their corresponding graph

Answer 1

equation a and graph E

equation b and graph a

equation c and graph b

equation d and graph D

Explanation:

Answer 2

Equation a
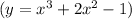`(\(y = x^3 + 2x^2 - 1\))` corresponds to graph E, b
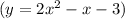`(\(y = 2x^2 - x - 3\))` to graph A, c
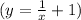`(\(y = (1)/(x) + 1\))` to graph B, and d
`(\(y = 2 - 3x^2 - x^3\))` to graph D.

Equation a,
`\(y = x^3 + 2x^2 - 1\)`, corresponds to graph E. The cubic term dominates, leading to a graph with both positive and negative inflections.

Equation b,
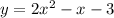`\(y = 2x^2 - x - 3\)`, pairs with graph A. This quadratic equation forms a parabola opening upwards with a clear minimum point.

Equation c,
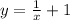`\(y = (1)/(x) + 1\)`, aligns with graph B. It represents a hyperbola, demonstrating reciprocal behavior with a vertical asymptote.

Equation d,
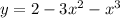`\(y = 2 - 3x^2 - x^3\)`, matches with graph D. This cubic equation exhibits a descending slope, capturing the characteristic shape of a cubic function.