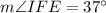Answer:
The length EI is;
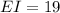
The measure of angle IFE is;
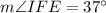
Step-by-step explanation:
Given the rectangle in the attached image.
Given;
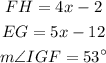
Recall that the length of the diagonals of a rectangle are equal so;

solving for x, we have;
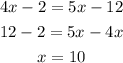
Since we have the value of x, let us substitute to get the length of diagonal EG;

Also, note that the diagonals of a rectangle bisect each other, so the length of EI would be;
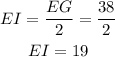
Therefore, the length EI is;
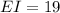
To get the measure of angle IFE;
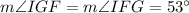
Reason: base angles of an isosceles triangle are equal.
So;

Reason: Complementary angles.
Substituting the value of angle IFG;

Therefore, the measure of angle IFE is;