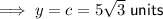Question

NO LINKS!!! URGENT HELP PLEASE!!!

Please help with the Special triangles #19, 21, and 23

Answer 1

Question 19:

• x = (9√6)/2 units
• y = (9√6)/2 units
• z = 18 units

Question 21:

• x = 6 units
• y = 6√3 units
• z = 6√6 units

Question 23:

• x = 10√3 units
• y = 5√3 units
• z = 15 units

Explanation:

45-45-90 triangle

A 45-45-90 triangle is a special right triangle where the measures of its sides are in the ratio 1 : 1 : √2. Therefore, the formula for the ratio of the sides is b : b : b√2 where:

• b is each side opposite the 45 degree angles (legs).
• b√2 is the side opposite the right angle (hypotenuse).

30-60-90 triangle

A 30-60-90 triangle is a special right triangle where the measures of its sides are in the ratio 1 : √3 : 2. Therefore, the formula for the ratio of the sides is c: c√3 : 2c where:

• c is the shortest side opposite the 30° angle.
• c√3 is the side opposite the 60° angle.
• 2c is the longest side (hypotenuse) opposite the right angle.

Question 19

Side z is the hypotenuse of a 30-60-90 triangle where the leg opposite the 30° angle measures 9 units. Therefore, c = 9.

`\implies z=2c =2 \cdot 9=18\; \sf units`

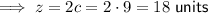
Therefore, the other leg of the same triangle (opposite the 60° angle) measures c√3 = 9√3 units.

Sides x and y are the congruent legs of a 45-45-90 triangle with hypotenuse measuring 9√3 units. Therefore b√2 = 9√3, so b = (9√6)/2.

`\implies x=(9 √(6))/(2)\; \sf units`

`\implies y=(9 √(6))/(2)\; \sf units`

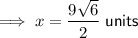
Question 21

Side x is the side opposite the 30° angle in a 30-60-90 triangle with a hypotenuse of 12 units. Therefore, 2c = 12 so c = 6.

`\implies x=6\; \sf units`

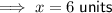
Therefore, the other leg of the same triangle (opposite the 60° angle) measures c√3 = 6√3 units.

Side y is one of the congruent legs of a 45-45-90 triangle where the other congruent leg measures 6√3 units.

`\implies y=6√(3)\; \sf units`

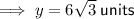
Side z is the hypotenuse of a 45-45-90 triangle where the congruent legs measure 6√3 units. Therefore b = 6√3.

`\implies z=b√(2) = 6 √(3) √(2)=6√(6)\; \sf units`

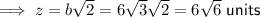
Question 23

Side z is one of the congruent legs of a 45-45-90 triangle where the hypotenuse measures 15√2 units. Therefore, b√2 = 15√2, so b = 15.

`\implies z=b=15\; \sf units`

Side x is the hypotenuse of a 30-60-90 triangle where the leg opposite the 60° measures 15 units. Therefore, c√3 = 15, so c = 5√3.

`\implies x=2c=2 \cdot 5√(3)=10√(3)\; \sf units`

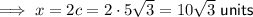
Side y is the side opposite the 30° angle in a 30-60-90 triangle where the hypotenuse measures 10√3 units. Therefore, 2c = 10√3, so c = 5√3.

`\implies y=c=5√(3)\; \sf units`

Answer 2

Answers:

`\begin{array}{llll} 19. & \text{x}= (9√(6))/(2), & \text{y}= (9√(6))/(2), & \text{z}= 18\\\\21. & \text{x}= 6, & \text{y}= 6√(3), & \text{z}= 6√(6)\\\\23. & \text{x}= 10√(3), & \text{y}= 5√(3), & \text{z}= 15\\\\\end{array}`

===========================================================

Work Shown:

Problem 19

The triangle up top is a 30-60-90 triangle. The short leg is opposite the smallest angle 30 degrees. Double the short leg to get the hypotenuse.

z = 2*9 = 18.

The long leg is found like so

`\text{long leg} = (\text{short leg})*√(3)\\\\\text{long leg} = 9√(3)\\\\`

These two formulas apply to 30-60-90 triangles only.

The long leg of the 30-60-90 triangle up top is the hypotenuse of the 45-45-90 triangle at the bottom.

For 45-45-90 triangles, we can say:

`\text{hypotenuse} = (\text{leg})*√(2)\\\\\text{leg} = \frac{\text{hypotenuse}}{√(2)}\\\\\text{leg} = \frac{\text{hypotenuse}*√(2)}{2}\\\\\text{leg} = (9√(3)*√(2))/(2)\\\\\text{leg} = (9√(3*2))/(2)\\\\\text{leg} = (9√(6))/(2)\\\\`

This represents the lengths of x and y. For any 45-45-90 triangle, the two legs are the same length (the right triangle is isosceles).

--------------------------------

Problem 21

Focus on the 30-60-90 triangle up top.

The hypotenuse of 12 divides in half to get x = 12/2 = 6 as the short leg.

The long leg is
`6√(3)`

This is also the leg of the 45-45-90 triangle down below. Therefore, we have
`y = 6√(3)`

Multiply the leg by sqrt(2) to find the hypotenuse.

`\text{hypotenuse} = \text{leg}*√(2)\\\\\text{z} = 6√(3)*√(2)\\\\\text{z} = 6√(3*2)\\\\\text{z} = 6√(6)\\\\`

--------------------------------

Problem 23

Focus on the triangle on the right. This is a 45-45-90 triangle.

The hypotenuse is 15sqrt(2), which must mean each leg is 15 units long. Therefore, z = 15. The unmarked vertical leg is also 15 units long.

This vertical side is the leg of the 30-60-90 triangle on the left. It's the long leg.

`\text{long leg} = (\text{short leg})*√(3)\\\\\text{short leg} = \frac{\text{long leg}}{√(3)}\\\\\text{short leg} = \frac{(\text{long leg})*√(3)}{3}\\\\\text{y} = (15√(3))/(3)\\\\\text{y} = 5√(3)\\\\`

Double this short leg to get the hypotenuse of the 30-60-90 triangle.

`x = 2y\\\\x = 2*5√(3)\\\\x = 10√(3)\\\\`