Question

Solve for w.
(w+5)² =2w² +3w+37

Answer 1

w = 3; w = 4

Explanation:

We can start by expanding the equation on the left hand side:

`(w+5)^2=2w^2+3w+37\\(w+5)(w+5)=2w^2+3w+37\\w^2+5w+5w+25=2w^2+3w+37\\w^2+10w+25=2w^2+3w+37`

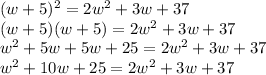
We can first simplify the equation subtracting all the terms on the right hand side and having the equation equal 0:

`w^2+10w+25=2w^2+3w+37\\(w^2-2w^2)+(10w-3w)+(25-37)=0\\-w^2+7w-12=0`

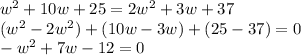
Now, we have one equation in standard form (ax^2 + bx + c = 0).

We can solve this equation using the quadratic equation which is

`x = (-b+√(b^2-4ac) )/(2a) \\\\x=(-b-√(b^2-4ac) )/(2a)`

Since -1 is our a value, 7 is our b, and -12 is c, we simply plug in our values and solve for x:

First x:

`x=(-7+√(7^2-4(-1)(-12)) )/(2(-1))\\ \\x=(-7+√(1) )/(-2)\\ \\x=(-7+1)/(-2)\\ \\x=(-6)/(-2)\\ \\x=3`

Second x:

`x=(-7-√(7^2-4(-1)(-12)) )/(2(-1))\\ \\x=(-7-√(1) )/(-2)\\ \\x=(-7-1)/(-2)\\ \\x=(-8)/(-2)\\ \\x=4`

Finally, we must check for extraneous solutions, which (if present) will make the equations not true. We simply plug in 3 for w and 4 for w to check for such solutions:

Checking 3:

`(3+5)^2=2(3)^2+3(3)+37\\8^2=2(9)+9+37\\64=18+9+37\\64=64`

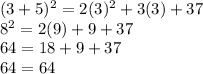
Checking 4:

`(4+5)^2=2(4)^2+3(4)+37\\9^2=2(16)+12+37\\81=32+12+37\\81=81`

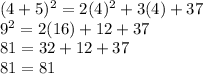
Since the equations are true for both 3 and 4, both values work for w.