Answer:
Total profit after 10 years =
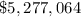
Explanation:
Let
 represent the profit in the nth year
represent the profit in the nth year
Then
 represents the profit in year
represents the profit in year
 1
1
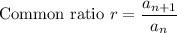
The sum of a geometric sequence is given by
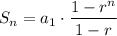
where
 first term
first term
 common ratio
common ratio
 number of terms
number of terms
Calculation of r
To calculate r we see that the profit increases by 16% every year
16% = 16/100 = 0.16
If profit increases by 0.16, then next year's profit
= this year's profit(1 + 0.16)
= this year's profit x 1.16
r = 1.16 the ratio of a term to the previous term
In this problem we are given the first term as

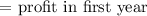
 number of years
number of years
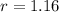
Plugging these values into equation [1] for the sum we get
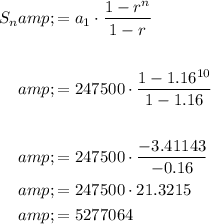
Therefore the total profit after 10 years
= $5,277,064