Question

NO LINKS!!!! URGENT HELP PLEASE!!!
Please help me with this Special Right Triangle: 45-45-90

Answer 1

* In a 45-45-90 degrees special right triangle, the length of the legs are equal.

For this triangle, we have:

Length of each leg = x

Length of hypotenuse= x √ 2


Therefore we have:

X √2 = 19


Solve for x by dividing both sides by

√ 2 :

X √ 2 / √ 2 = 19 / √ 2


X= 19 / √2


Since the length of the legs are equal, the value of y is:

Y= 19 / √ 2


Solutions:

X= 19 / √ 2

Y= 19 / √ 2

Answer 2

x = 13.44 (2 d.p.)

y = 13.44 (2 d.p.)

Explanation:

The interior angles of a triangle sum to 180°. Therefore, the missing angle of the given triangle is 45°. This means the triangle is a 45-45-90 triangle.

What is a 45-45-90 triangle?

A 45-45-90 triangle is a special right triangle in that the measures of its sides are in the proportion x : x : x√2 where:

• x are the sides opposite the 45 degree angles (legs).
• x√2 is the side opposite the right angle (hypotenuse).

As the given triangle is a 45-45-90 triangle, sides x and y are the same length.

As the hypotenuse (side opposite the right angle) is 19 units in length, then x√2 = 19. To find the length of x (and y), solve for x:

`\implies x√(2) = 19`

`\implies (x√(2))/(√(2)) = (19)/(√(2))`

`\implies x= (19√(2))/(2)`

`\implies x=13.44\; \sf units\;(2\;d.p.)`

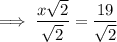
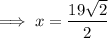
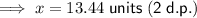
Solution

• x = 13.44 (2 d.p.)
• y = 13.44 (2 d.p.)