Question

A coordinate grid is mapped on a video game screen, with the origin in the lower-left corner. A game designer programs a helicopter to follow a path that can be modeled by a quadratic function with a vertex at (16, 20) and passing through the point (4, 25). She also programs an airplane to move along a linear path that passes through the points (0, 18) and (30, 20). Which system of equations can be used to determine whether the paths of the helicopter and airplane cross?

StartLayout Enlarged Left-Brace 1st Row y = one-fifteenth x + 18 2nd Row y = StartFraction 5 Over 144 EndFraction (x minus 16) squared + 20 EndLayout
StartLayout Enlarged Left-Brace 1st Row y = 15 x + 18 2nd Row y = StartFraction 5 Over 144 EndFraction (x minus 16) squared + 20 EndLayout
StartLayout Enlarged Left-Brace 1st Row y = one-fifteenth x + 18 2nd Row y = Negative StartFraction 5 Over 144 EndFraction (x minus 4) squared + 25 EndLayout
StartLayout Enlarged Left-Brace 1st Row y = 15 x + 18 2nd Row y = Negative StartFraction 5 Over 144 EndFraction (x minus 4) squared + 25 EndLayout

Answer 1

A

Explanation:

<3

Answer 2

1) y = (1/15)x + 18

2) y = (5/144) (x - 16)^2 + 20

Solution:

1) The solution consists in establishing the equations that model the two paths.

2) Let's start with the easiest one. It is the linear path.

You have that the equation is a line that passes through the points (0,18) and (30,20). This equation is found using this formula:

`(y-b)/(x-a) =(d-b)/(c-a)`

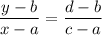
where the two points are (a,b) and (c,d)

So, for the two points given:

`(y-18)/(x-0) =(20-18)/(30-0) =(2)/(30)`

=>
`(y - 18)*30 = x*2`

=>
`30y - 540 = 2x`

=>
`30y = 2x + 540`

=>
`y = 2x / 30 + 540 / 30`

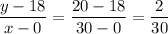
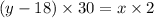
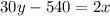
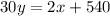
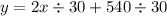
=> y = x/15 + 18 ---------------> this is the first equation of the system.

3) Now, find the equation for the path modeled by the quadratic function.

The vertex form of a quadratic function is:
`y = A (x - h)^2 + k`

where the vertex is (k,h).

Then, so far you can write
`y = A (x - 16)^2 + 20`

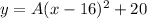
Now, replace the coordinates of the point (4,25) to find the value of A:

`25 = A (4 - 16)^2 + 20`

=>
`25 = A (-12)^2 + 20`

=>
`25 = A*144 + 20`

=>
`144A = 25 - 20`

=>
`144\ A = 5`

=>
`A = 5 / 144`

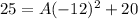
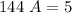
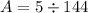
=> y = (5 / 144) (x - 16)^2 + 20 ---------> this is the second equation of the system.

System:

1)
`y = ((1)/(15) )x + 18`

2)
`y = ((5)/(144) )\ (x - 16)^2 + 20`