Question

Hi find the distance in the coordanite plane between the two points and show ur work

1 (5, -8) and (5,2)


2 (-8, -2) and (7, -2)


3 (9, 10) and (9, -2)


4 (11 , 6) and (-7, 6)

Answer 1

The distance between (5, -8) and (5,2) is: d = 10 units

Explanation:

Note: I will solve the first question as the procedure solution for the remaining questions is exactly the same.

Given the points

• (5, -8)

• (5,2)

Determining the distance between (5, -8) and (5,2)

`d=√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

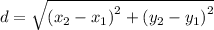
substitute (x₁, y₁) = (2, 3) and (x₂, y₂) = (2, -5)

`=√(\left(5-5\right)^2+\left(2-\left(-8\right)\right)^2)`

`=√(\left(5-5\right)^2+\left(2+8\right)^2)`

`=√(0+10^2)`

`=√(10^2)`

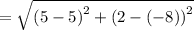
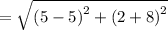
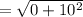
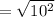
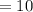`=10` units

Therefore, the distance between (5, -8) and (5,2) is: d = 10 units