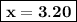Question

Hi, can you please help with math, I think the exercise solving is probably with x and y. Thank u very much:)

1. Two identical jars of cottage cheese and 3 buns of the same type cost 10 euros. A jar of cottage cheese is 2 euros more expensive than a bun. How much is a jar of cottage cheese and how much is a bun?

Again, Thank u!​

Answer 1

A jar of cottage cheese is €3.20

A bun is €1.20

Explanation:

Let

x = Cost of a jar of cottage cheese (euros)

y = Cost of a bun (euros)

Step I:

Translate the statements mathematically:
2 jars of cottage cheese cost =
`2x` euros

3 buns cost =
`3y` euros
∴ Total cost =
`2x + 3y = 10` euros

A jar of cottage cheese is 2 euros more expensive than a bun:
`x = 2 + y`

Step II:

A system of linear simultaneous equations:

`x = 2 + y` ——(equation i)

`2x + 3y = 10` ———-(equation ii)

Step III:

Solve the linear simultaneous equations either by the substitution, elimination or graphical method

Substitution method:

Substitute (equation i) into (equation ii) and solve for y:

`2(2 + y) + 3y = 10`

Expand the parenthesis and make y the subject of the equation:

`4 + 2y + 3y = 10`

`2y + 3y = 10 - 4`

`5y = 6`

`y = (6)/(5)`

∴y = Cost of a bun = €1.20 (One euro and 20 cents)

Substitute this value of y in any of the equations to solve for x:

`x = 2 + 1.20`

∴x = Cost of a jar = €3.20(Three euros and 20 cents)

Answer 2

Cost of jar of cottage cheese = € 3.20

Cost of a bun = € 1.20

Explanation:

Framing and solving system of linear equations:

Let the cost of 1 jar of cottage cheese = x

Let the cost of 1 bun = y

Cost of 2 jar of cottage cheese = 2x

Cost of 3 bun = 3y

Cost of 2 jars of cottage cheese + cost of 3 buns = € 10

2x + 3y = 10 ------------------(I)

Cost of a jar of cottage cheese = 2 + cost of a bun

x = 2 + y ----------------(II)

Substitute x = 2 + y in equation (I),

2*(2+y) + 3y = 10

Use distributive property,

2*2 + 2*y + 3y = 10

4 + 2y + 3y = 10

Combine like terms,

4 + 5y = 10

Subtract 4 from both sides,

5y = 10 - 4

5y = 6

Divide both sides by 5

y = 6 ÷ 5

`\boxed{\bf y = 1.20}`

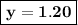
Substitute y = 1.2 in equation (II),

x = 2 + 1.2

`\boxed{\bf x = 3.20}`