Question

The variance will reach a maximum in a binomial distribution when

Answer 1

Third choice
π = 1/2 and 1 - π = 1/2

Explanation:

Formula for binomial distribution is

`P(x) = (n!)/(x!(n-x)!) \pi^x (1-\pi)^(n-x)`

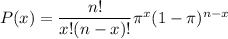
where
x is the number of successes

n = number of trials

π = probability of success on a single trial

The variance of the binomial distribution is

`\sigma^2 = n \cdot \pi(1-\pi)`

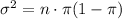
The maximum variance occurs when

`\pi = (1- \pi) = 1/2`

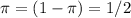
Hence the correct choice is the third choice
π = 1/2 and 1- π = 1/2